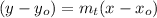Question

The curve given by:

x=sin(????); y=sin(????+sin(????))
has two tangent lines at the point (x,y)=(0,0).
List both of them in order of increasing slope. Your answers should be in the form of y=????(x) without ????′????.

Answer 1

Equations of tangent lines are

y= 2 x

y = 0

Explanation:

x = sin t -- (1)

y = sin(t + sin(t)) -- (2)

Differentiating both equations w.r.to t to find slopes.

`(dx)/(dt)=(d(sin(t)))/(dt)\\\\(dx)/(dt)=cos(t)--(3)`

`(dy)/(dt)=(d)/(dt)(sin(t+sin(t))\\\\(dy)/(dt)=cos(t+sin(t))(d)/(dt)(t+sin(t))\\\\(dy)/(dt)=cos(t+sin(t)(1+cos(t))\\\\(dy)/(dt)=(1+cos(t))cos(t+sin(t))--(4)`

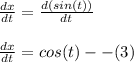
Dividing (2) by (1) to find slope

`(dy)/(dx)=((1+cos(t))cos(t+sin(t)))/(cos(t))\\`

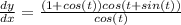
at tangent point x=y=0

From (1)

sin (t) = 0

⇒ t = 0, π

At t = 0

`(dy)/(dx)\Big|_(t=0)=((1+cos(t))cos(t+sin(t)))/(cos(t))\\\\\\(dy)/(dx)\Big|_(t=0)=((1+cos(0))cos(0+sin(0)))/(cos(0))\\\\\\(dy)/(dx)\Big|_(t=0)=((1+1)cos(0+0))/(1)\\\\\\(dy)/(dx)\Big|_(t=0)=2\\`

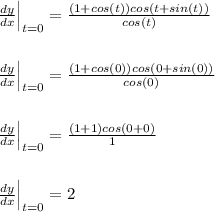
At t= π

`(dy)/(dx)\Big|_(t=\pi)=((1+cos(t))cos(t+sin(t)))/(cos(t))\\\\\\(dy)/(dx)\Big|_(t=\pi)=((1+cos(\pi))cos(\pi+sin(\pi)))/(cos(\pi))\\\\\\(dy)/(dx)\Big|_(t=\pi)=((1-1)cos(\pi+0))/(-1)\\\\\\(dy)/(dx)\Big|_(t=\pi)=0\\`

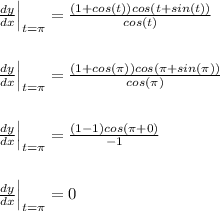
Equation of tangent

`(y-y_o)=m_t(x-x_o)\\`

`Tangent\,\,point=(x_o,y_o)=(0,0)\\\\For\,\,t=0\\\\(y-0)=(2)(x-0)\\\\y=2x\\\\for\,\,t=\pi\\\\(y-0)=(0)(x-0)\\\\y=0`