Question

A baseball pitcher throws a baseball horizontally at a linear speed of 42.5 m/s (about 95 mi/h). Before being caught, the baseball travels a horizontal distance of 16.0 m and rotates through an angle of 44.5 rad. The baseball has a radius of 3.67 cm and is rotating about an axis as it travels, much like the earth does. What is the tangential speed of a point on the "equator" of the baseball?

Answer 1

The tangential speed of a point on the "equator" of the baseball is 4.33 m/s.

Step-by-step explanation:

Given that,

Linear speed of base ball = 42.5 m/s

Distance = 16.0 m

Angle = 44.5 rad

Radius of baseball = 3.67 cm

We need to calculate the flight time

Using formula of time

`t=(d)/(v)`

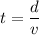
Put the value into the formula

`t=(16.0)/(42.5)`

`t=0.376\ sec`

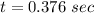
We need to calculate the number of rotation

Using formula of number of rotation

`n=\theta\time 2\pi`

`n=(44.5)/(2\pi)`

`n=7.08`

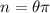
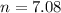
We need to calculate the time for one rotation

Using formula of time

`T=(t)/(n)`

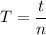
Put the value into the formula

`T=(0.376)/(7.08)`

`T=0.053\ sec`

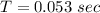
We need to calculate the circumference

Using formula of circumference

`C=2\pi* r`

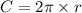
Put the value into the formula

`C=2\pi*3.67*10^(-2)`

`C=0.23\ m`

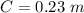
The tangential speed is equal to the circumference divided by the time. it takes to complete one rotation.

We need to calculate the tangential speed

Using formula of tangential speed

`v=(C)/(T)`

Put the value into the formula

`v=(0.23)/(0.053)`

`v=4.33\ m/s`

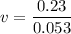
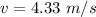
Hence, The tangential speed of a point on the "equator" of the baseball is 4.33 m/s.