Answer:
The greatest possible value for b is 26.
Explanation:
Given that the line passes through the Origin O(0, 0); A(-2, b - 14) &
B(14 - b, 72).
Let us assume the points are in the order: AOB.
Since the line passes through all these points the slope of the line segment AO = The slope of the line segment AB.
Slope of a line with two points:
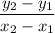 where
where
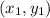 and
and
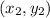 are the points given.
are the points given.
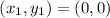

Therefore, the slope of the line segment AO =
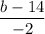
Similarly, for the slope of the line segment OB.
The two points are
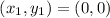 and
and
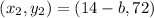 .
.
The slope is:
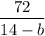
Since, the slopes are equal we can equate:
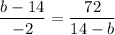
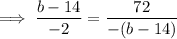
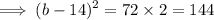
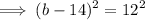
Taking square root on both sides we get:
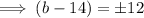
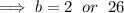
Therefore, the maximum value of b = 26.
Hence, the answer.