Question

A group of concerned citizens has established a trust fund that pays 5% interest, compounded monthly, to preserve a historical buildingby providing annual maintenance funds of $80,000 forever. Compute the capitalized equivalent amount for these building maintenance expenses.

Answer 1

The value of the stablish fund is 1,563,663.64 dollars

Step-by-step explanation:

First, we solve for the effective annual rate as this is a rate which compounds monthly:

`(1+APR/m)^m-1 = r_e\\(1+0.05/12)^(12) - 1 = r_e\\r_e = 0.051161898`

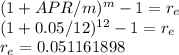
Now, we solve for the Principal of a perpetuity which interest over the year are 80,000:

`(Annuity)/(Principal) = rate\\Principal = Annuity / rate\\Principal = 80,000 / 0.051161898`

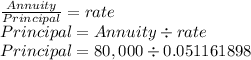
Principal = 1.563.663,64