Question

According to data from the state blood program, 40 percent of all individuals have group A blood. If six individuals give blood, find the probability that exactly three of the individuals have group A blood.

Answer 1

Answer: 0.27648

Explanation:

Given : The proportion of all individuals have group A blood : p=0.040

Total individuals give blood : n= 6

Let X be the number of individuals have group A blood.

Since all individual are independent of each other.

`X\sim Bin(n=6, p=0.40)`

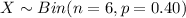
Formula :
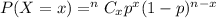`P(X=x)=^nC_xp^x(1-p)^(n-x)` , where n= sample size , p = probability of getting success in each trial.

The probability that exactly three of the individuals have group A blood. :

`P(x=3)= ^6C_3(0.40)^3(1-0.4)^3\\\\= (6!)/(3!3!)*(0.40)^3(0.60)^3\\\\=0.27648`

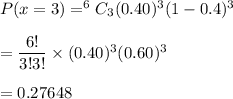
The probability that exactly three of the individuals have group A blood. is 0.27648