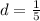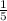
Common difference of the given arithmetic sequence is equal to
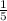
Explanation:
The given arithmetic sequence is in mixed numbers. Converting them into proper fractions, we get:
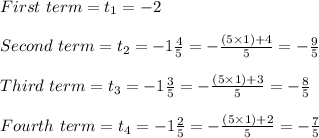
The sequence can thus be rewritten as
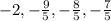
To find the common difference of the given arithmetic sequence, subtract any two consecutive numbers of the sequence. The difference between two consecutive numbers is always a constant and is termed as the common difference.
Hence,
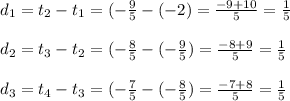

Common difference