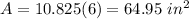Question

Hi, please help and explain! :)

What is the area of a regular hexagon with a side length of 5in and an apothem of 4.33in?

Answer 1

`A=64.95\ in^2`

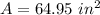
Explanation:

we know that

A regular hexagon can be divided into six equilateral triangles

so

The area of a regular hexagon is the same that the area of six congruent equilateral triangles

The area of one equilateral triangle in the regular hexagon is equal to

`A=(1)/(2)(b)(h)`

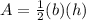
where

b is the base of triangle (the length of the regular hexagon)

h is the height of triangle (the apothem of the regular hexagon)

so

`b=5\ in\\h=4.33\ in`

substitute

`A=(1)/(2)(5)(4.33)=10.825\ in^2`

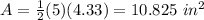
Multiply the area of one triangle by 6 to obtain the area of the regular hexagon

`A=10.825(6)=64.95\ in^2`