Answer:
The required probability is
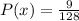 or
or
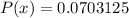 .
.
Explanation:
Consider the provided information.
A committee of 9 members is voting on a proposal. Each member casts a yea or nay vote. On a random voting basis,
The probability of yea or nay vote is equal, =

So, we can say that
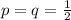
Use the formula:
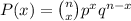
Where n is the total number of trials, x is the number of successes, p is the probability of getting a success and q is the probability of failure.
We want proposal wins by a vote of 7 to 2, that means the value of x is 7.
Substitute the respective values in the above formula.
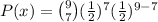
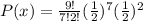
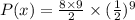
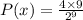
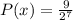
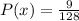 or
or
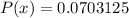
Hence, the required probability is
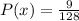 or
or
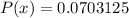 .
.