Answer:
(a). The velocity of bus at 2.0 sec is 6.8 m/s.
(b). The position of bus at 2.0 s is 11.8 m.
(c).
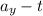 ,
,
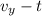 and x-t graphs
and x-t graphs
Step-by-step explanation:
Given that,
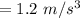
Time t = 1.0 s
Velocity = 5.0
The Acceleration equation is
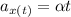
We need to calculate the velocity
Using formula of acceleration
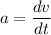
On integrating
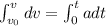
Put the value into the formula

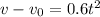
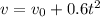
Put the value into the formula
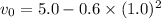
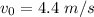
We need to calculate the velocity at 2.0 sec
Put the value of initial velocity in the equation
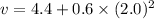
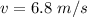
(b). If the bus’s position at time t = 1.0 s is 6.0 m,
We need to calculate the position
Using formula of velocity

On integrating
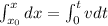

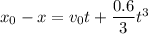
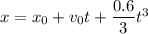
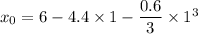
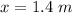
The position at t = 2.0 s
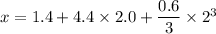
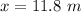
Hence, (a). The velocity of bus at 2.0 sec is 6.8 m/s.
(b). The position of bus at 2.0 s is 11.8 m.
(c).
 ,
,
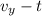 and x-t graphs
and x-t graphs