Question

How strong an electric field is needed to accelerate electrons in an X-ray tube from rest to one-tenth the speed of light in a distance of 5.1 cm?

Answer 1

E= 50.1*10³ N/C

Step-by-step explanation:

Assuming no other forces acting on the electron, if the acceleration is constant, we can use the following kinematic equation in order to find the magnitude of the acceleration:

`vf^(2) -vo^(2) = 2*a*x`

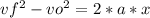
We know that v₀ = 0 (it starts from rest), that vf = 0.1*c, and that x = 0.051 m, so we can solve for a, as follows:

`a = (vf^(2))/(2*x) = ((3e7 m/s)^(2) )/(2*0.051m) =8.8e15 m/s2`

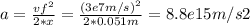
According to Newton's 2nd Law, this acceleration must be produced by a net force, acting on the electron.

Assuming no other forces present, this force must be due to the electric field, and by definition of electric field, is as follows:

F = q*E (1)

In this case, q=e= 1.6*10⁻19 C

But this force, can be expressed in this way, according Newton's 2nd Law:

F = m*a (2) ,

where m= me = 9.1*10⁻³¹ kg, and a = 8.8*10¹⁵ m/s², as we have just found out.

From (1) and (2), we can solve for E, as follows:

`E=(me*a)/(e) =((9.1e-31 kg)*(8.8e15m/s2))/(1.6e-19C) = 50.1e3 N/C`

⇒ E = 50.1*10³ N/C