Answer:
a)
![E(\hat \theta_1) =(1)/(2) [E(X_1) +E(X_2)]= (1)/(2) [\mu + \mu] = \mu](https://img.qammunity.org/2021/formulas/mathematics/college/r1trrhnxk7nxulmvjwph7yc89ekghwoll3.png)
So then we conclude that
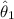 is an unbiased estimator of
is an unbiased estimator of

![E(\hat \theta_2) =(1)/(4) [E(X_1) +3E(X_2)]= (1)/(4) [\mu + 3\mu] = \mu](https://img.qammunity.org/2021/formulas/mathematics/college/4b0xsq4n8tmr8c2bfwsbf0140zcuiz8t39.png)
So then we conclude that
 is an unbiased estimator of
is an unbiased estimator of

b)
![Var(\hat \theta_1) =(1)/(4) [\sigma^2 + \sigma^2 ] =(\sigma^2)/(2)](https://img.qammunity.org/2021/formulas/mathematics/college/zto012h7j17gngcovk6z8pc6phd16zk10f.png)
![Var(\hat \theta_2) =(1)/(16) [\sigma^2 + 9\sigma^2 ] =(5\sigma^2)/(8)](https://img.qammunity.org/2021/formulas/mathematics/college/uynonwak79m85xwh4rvmxs38jtnga4604m.png)
Explanation:
For this case we know that we have two random variables:
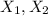 both with mean
both with mean
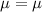 and variance
and variance
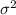
And we define the following estimators:
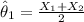
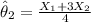
Part a
In order to see if both estimators are unbiased we need to proof if the expected value of the estimators are equal to the real value of the parameter:
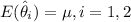
So let's find the expected values for each estimator:

Using properties of expected value we have this:
![E(\hat \theta_1) =(1)/(2) [E(X_1) +E(X_2)]= (1)/(2) [\mu + \mu] = \mu](https://img.qammunity.org/2021/formulas/mathematics/college/r1trrhnxk7nxulmvjwph7yc89ekghwoll3.png)
So then we conclude that
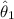 is an unbiased estimator of
is an unbiased estimator of

For the second estimator we have:
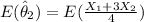
Using properties of expected value we have this:
![E(\hat \theta_2) =(1)/(4) [E(X_1) +3E(X_2)]= (1)/(4) [\mu + 3\mu] = \mu](https://img.qammunity.org/2021/formulas/mathematics/college/4b0xsq4n8tmr8c2bfwsbf0140zcuiz8t39.png)
So then we conclude that
 is an unbiased estimator of
is an unbiased estimator of

Part b
For the variance we need to remember this property: If a is a constant and X a random variable then:

For the first estimator we have:
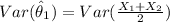
![Var(\hat \theta_1) =(1)/(4) Var(X_1 +X_2)=(1)/(4) [Var(X_1) + Var(X_2) + 2 Cov (X_1 , X_2)]](https://img.qammunity.org/2021/formulas/mathematics/college/64n4u9wwwqo5nhckviyw06b8b1v4qorrp4.png)
Since both random variables are independent we know that
 so then we have:
so then we have:
![Var(\hat \theta_1) =(1)/(4) [\sigma^2 + \sigma^2 ] =(\sigma^2)/(2)](https://img.qammunity.org/2021/formulas/mathematics/college/zto012h7j17gngcovk6z8pc6phd16zk10f.png)
For the second estimator we have:

![Var(\hat \theta_2) =(1)/(16) Var(X_1 +3X_2)=(1)/(4) [Var(X_1) + Var(3X_2) + 2 Cov (X_1 , 3X_2)]](https://img.qammunity.org/2021/formulas/mathematics/college/cnq82fumuoxfdz07afjvstkvpmjilfx9yl.png)
Since both random variables are independent we know that
 so then we have:
so then we have:
![Var(\hat \theta_2) =(1)/(16) [\sigma^2 + 9\sigma^2 ] =(5\sigma^2)/(8)](https://img.qammunity.org/2021/formulas/mathematics/college/uynonwak79m85xwh4rvmxs38jtnga4604m.png)