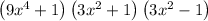The complete factorized form for the given expression is
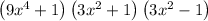
Explanation:
Step 1: Given expression:
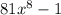
Step 2: Trying to factor as a Difference of Squares
Factoring
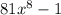
As we know the theory that the difference of two perfect squares,
 can be factored into (A+B) (A-B)
can be factored into (A+B) (A-B)
from this, when analysing, 81 is the square of 9,
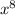 is the square of
is the square of
 . Hence, we can write the given expression as,
. Hence, we can write the given expression as,

By using the theory, we get
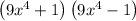
Again, we can further factorise the term
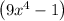
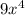 is the square of
is the square of
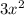 . Therefore, it can be expressed as below
. Therefore, it can be expressed as below
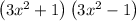
Now, we can not factorise further the term
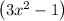 . Because it will come as
. Because it will come as
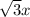 (3 is not a square term). Thereby concluding that the complete factorisation for the given expression is
(3 is not a square term). Thereby concluding that the complete factorisation for the given expression is