Answer:
![\sqrt[4]{e};\frac1{4e}](https://img.qammunity.org/2023/formulas/mathematics/high-school/pjcb1gus581esw92ucta34bmyeo0smvywc.png)
Step-by-step explanation:
The first derivative of
 will give, for each x, the slope of the tangent at that specific x. Let's calculate the derivative, applying the quotient rule.
will give, for each x, the slope of the tangent at that specific x. Let's calculate the derivative, applying the quotient rule.
![D(\frac AB) = (A'B-AB')/(B^2)\\f'(x)= \frac1{x^8}[(\frac1x)x^4-(lnx)(4x^3)]=\frac1{x^8}[x^3(1-4lnx)]=(1-4lnx)/(x^5)](https://img.qammunity.org/2023/formulas/mathematics/high-school/ffe0ha69oj6ffnimjhiv2be97yy8ymdvvo.png)
Now, to find the point with an horizontal tangent (called "stationary points"), we set the first derivative equal to 0. Considering that we're working with
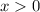 we deal only with the numerator.
we deal only with the numerator.
![1-4lnx = 0 \rightarrow lnx= \frac14\\x=e^\frac14 =\sqrt[4]{e}](https://img.qammunity.org/2023/formulas/mathematics/high-school/hmdtrxgeslmcw75shmqcl7qd9thi7c3epm.png)
At this point we Replace the value we found in the equation to find it's y coordinate
![f(\sqrt[4]e) = (ln\sqrt[4]e)/(\sqrt[4]e^4)= (\frac14)/(e) = \frac1{4e}](https://img.qammunity.org/2023/formulas/mathematics/high-school/9jef7sdfz9708161cje0bgcppgpvhs8ier.png)