Question

The accompanying frequency distribution represents the square footage of a random sample of 500 houses that are owner occupied year round. Approximate the mean and standard deviation square footage. statcrunch

Square footage Frequency 0- 499 500 999 13 1,000 1.499 33 1,500 1.999 115 2,000- 2.499 125 2,500 2.999 81 3,000- 3.499 3,500- 3.999 45 4,000 4.499 22 4,500 4.999 10

Answer 1

`\bar X = (\sum_(i=1)^n x_i f_i)/(n) = (1220750)/(500)=2441.5`

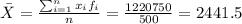
`s= \sqrt{(N \sum x^2 f -[\sum xf]^2)/(N(N-1)}= \sqrt{(500*3408029125 -[1220750]^2)/(50*49)}=9341.2405`

Explanation:

In order to find the mean and standard deviation we can create the following table:

Limits Frequency(f) x(midpoint) x*f x^2 *f

__________________________________________________

0-499 9 249.5 2245.5 560252.3

500-999 13 749.5 9743.5 7302753

1000-1499 33 1249.5 41233.5 51521258.25

1500-1999 115 1749.5 201192.5 351986278.8

2000-2499 125 2249.5 281187.5 632531281.3

2500-2999 81 2749.5 222709.5 612339770.3

3000-3499 47 3249.5 152726.5 496284761.8

3500-3999 45 3749.5 168727.5 632643761.3

4000-4499 22 4249.5 93489 397281505.5

4500-4999 10 4749.5 47495 225577502.5

_____________________________________________________

Total 500 1220750 3408029125

We can calculate the mean with the following formula:

`\bar X = (\sum_(i=1)^n x_i f_i)/(n) = (1220750)/(500)=2441.5`

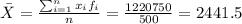
And the standard deviation would be given by:

`s= \sqrt{(N \sum x^2 f -[\sum xf]^2)/(N(N-1)}= \sqrt{(500*3408029125 -[1220750]^2)/(50*49)}=9341.2405`