Step-by-step explanation:
(a) It is known that equation for transverse wave is given as follows.
y =

Now, we will compare above equation with the standard form of transeverse wave equation,
y =
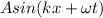
where, A is the amplitude = 0.09 m
k is the wave vector =
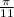
 is the angular frequency =
is the angular frequency =

x is displacement = 1.40 m
t is the time = 0.16 s
Now, we will differentiate the equation with respect to t as follows.
The speed of the wave will be:
v(t) =
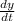
v(t) =
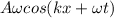
v(t) =

v(t) = -0.84 m/s
The acceleration of the particle in the location is
a(t) =
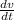
a(t) =
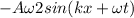
a(t) =
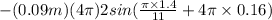
a(t) = -9.49
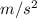
Hence, the value of transverse wave is 0.84 m/s and the value of acceleration is 9.49
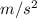 .
.
(b) Wavelength of the wave is given as follows.
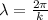
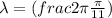
 = 22 m
= 22 m
The period of the wave is
T =
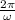
T =
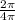
= 0.5 sec
Now, we will calculate the speed of propagation of wave as follows.
v =
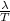
=
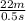
= 44 m/s
therefore, we can conclude that wavelength is 22 m, period is 0.5 sec, and speed of propagation of wave is 44 m/s.