Answer:
The probability of flipping Heads at least once is
 .
.
Explanation:
The probability of an event, say E, is the ratio of the favorable outcomes to the total number of outcomes, i.e.
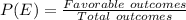
The sample space of flipping two coins is:
S = {HH, HT, TH and TH}
Total number of outcomes = 4
Compute the probability of flipping Heads at least once as follows:
Let X = heads.
P (X ≥ 1) = P (X = 1) + P (X = 2)
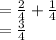
Thus, the probability of flipping Heads at least once is
 .
.
The experiment of flipping a coin is a binomial experiment.
Since there are only two outcomes of the experiment, either a Heads or a Tails.
So if X is defined as the number of heads in n flips of a coin then the random variable X follows a binomial distribution with probability p = 0.5 of success.