Question

to find the probability of flipping heads at least once if you flip a coin two times. The possible outcomes (we don't care about the order) are (each equally likely) TT, TH, HT, HH. Three out of four have an H in them, so the probability is 34. Is this correct? Is there a better and efficient way (especially when dealing with a higher number of flips? Please use only very basic terminology and concepts from probability because I've never taken a class.

Answer 1

The probability of flipping Heads at least once is
`(3)/(4)`.

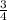Explanation:

The probability of an event, say E, is the ratio of the favorable outcomes to the total number of outcomes, i.e.

`P (E) = (Favorable\ outcomes)/(Total\ outcomes)`

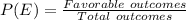
The sample space of flipping two coins is:

S = {HH, HT, TH and TH}

Total number of outcomes = 4

Compute the probability of flipping Heads at least once as follows:

Let X = heads.

P (X ≥ 1) = P (X = 1) + P (X = 2)

`=(2)/(4)+(1)/(4) \\=(3)/(4)`

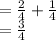
Thus, the probability of flipping Heads at least once is
`(3)/(4)`.

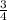The experiment of flipping a coin is a binomial experiment.

Since there are only two outcomes of the experiment, either a Heads or a Tails.

So if X is defined as the number of heads in n flips of a coin then the random variable X follows a binomial distribution with probability p = 0.5 of success.