Question

During an auto accident, the vehicle’s air bags deploy and slow down the passengers more gently than if they had hit the windshield or steering wheel. According to safety standards, air bags produce a maximum acceleration of 60 g that lasts for only 36 ms (or less). How far (in meters) does a person travel in coming to a complete stop in 36 ms at a constant acceleration of 60 g?

Answer 1

A person travels 39 cm in coming to a complete stop in 36 ms at a constant acceleration of 60 g.

Step-by-step explanation:

Hi there!

The equation of position of an object moving in a straight line at constant acceleration is the following:

x = x0 + v0 · t + 1/2 · a · t²

Where:

x = position at time t.

x0 = initial position.

v0 = initial velocity.

a = acceleration.

t = time.

So, let's see how much distance the person moves inside the car. Let's imagine that the person is initially at rest and suddenly is accelerated at 60 g (60 · 10 m/s² = 600 m/s²). In this case, x0 and v0 = 0 and the traveled distance will be:

x = 1/2 · 600 m/s² · (0.036)²

x = 0.39 m or 39 cm

Here, we have calculated the distance traveled by a person accelerated at 60 g from rest in 36 ms. Notice that the distance is the same if we calculate the traveled distance of a person that is brought to rest in 36 ms with an acceleration of 60 g.

A person travels 39 cm in coming to a complete stop in 36 ms at a constant acceleration of 60 g.

Answer 2

d = 0.38 m

Step-by-step explanation:

As we know that the person due to the airbag action, comes to a complete stop, in 36 msec or less, and during this time, is decelerated at a constant rate of 60 g, we can find the initial velocity (when airbag starts to work), as follows:

vf = v₀ -a*t

If vf = 0, we can solve for v₀:

v₀ = a*t = 60*9.8 m/s²*36*10⁻³s = 21.2 m/s

With the values of v₀, a and t, we can find Δx, applying any kinematic equation that relates all of some of these parameters with the displacement.

Just for simplicity, we can use the following equation:

`vf^(2) -vo^(2) = 2*a*d`

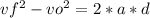
where vf=0, v₀ =21.2 m/s and a= -588 m/s².

Solving for d:

`d = (-vo^(2))/(2*a) = ((21.2m/s)^(2) )/(2*588 m/s2) =0.38 m`

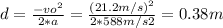
⇒ d = 0.38 m