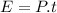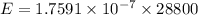Question

An 8 hour exposure to a sound intensity level of 95.0 dB may cause hearing damage. What energy in joules falls on a 0.850 cm diameter eardrum so exposed?

Answer 1

`E=5.0662* 10^(-3)\ J`

Step-by-step explanation:

Given:

• time of exposure of eardrum to the specific sound,
  `t=8\ hr=28800\ s`

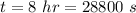
• intensity of the sound,
  `\beta=95\ dB`

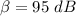
• diameter of the eardrum,
  `d=0.85\ cm=0.0085\ cm`

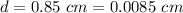
We have the relation between the flux density of the sound energy as:

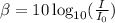`\beta=10\log_(10)((I)/(I_0) )` ................(1)

where:

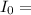`I_0=` the minimum flux density of sound energy just audible to human ears
`=10^(-12)`
`W.m^(-2)`

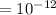
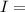`I=` the flux density of the sound energy due to the given intensity of sound

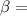`\beta=` given intensity of sound in decibels

from eq. (1) we've:

`95=10* \log_(10) ((I)/(10^(-12)) )`

`I=0.0031\ W.m^(-2)`

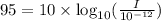
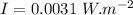
The above value is Power per unit area.

We now find the area of eardrum:

`A=(\pi.d^2)/(4)`

`A=(\pi* 0.0085^2)/(4)`

`A=5.67* 10^(-5)\ m^2`

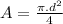
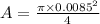
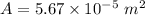
Now the energy reaching the eardrum per second is:

`P=I* A`

`P=0.0031* 5.67* 10^(-5)`

`P=1.7591* 10^(-7)\ W`

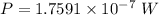
Now the total energy reaching the eardrum in the given time:

`E=P.t`

`E=1.7591* 10^(-7)* 28800`

`E=5.0662* 10^(-3)\ J`