Question

2. In a recent survey conducted by the International Nanny Association, 4,176 nannies were placed in a job in a given year. Only 24 of the nannies placed were men. Find the probability that a randomly selected nanny who was placed during the last year is a male nanny (a "mannie").

Answer 1

There is a 0.57% probability that a randomly selected nanny who was placed during the last year is a male nanny (a "mannie").

Explanation:

A probability is the number of desired outcomes divided by the number of total outcomes.

In this problem, we have that:

Desired outcomes:

The number of male nannies selected. 24 of the nannies placed were men. So the number of desired outcomes is 24.

Total outcomes:

The number of nannies selected. 4,176 nannies were placed in a job in a given year. So the number of total outcomes 4176.

Find the probability that a randomly selected nanny who was placed during the last year is a male nanny (a "mannie").

`P = (24)/(4176) = 0.0057`

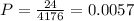
There is a 0.57% probability that a randomly selected nanny who was placed during the last year is a male nanny (a "mannie").