Question

The manufacturer of a CD player has found that the revenue R​ (in dollars) is Upper R (p )equals negative 5 p squared plus 1 comma 550 p comma when the unit price is p dollars. If the manufacturer sets the price p to maximize​ revenue, what is the maximum revenue to the nearest whole​ dollar? A. ​$961 comma 000

Answer 1

The maximum revenue is $1,20,125 that occurs when the unit price is $155.

Explanation:

The revenue function is given as:

`R(p) = -5p^2 + 1550p`

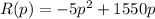
where p is unit price in dollars.

First, we differentiate R(p) with respect to p, to get,

`(d(R(p)))/(dp) = (d(-5p^2 + 1550p))/(dp) = -10p + 1550`

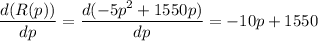
Equating the first derivative to zero, we get,

`(d(R(p)))/(dp) = 0\\\\-10p + 1550 = 0\\\\p = (-1550)/(-10) = 155`

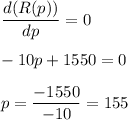
Again differentiation R(p), with respect to p, we get,

`(d^2(R(p)))/(dp^2) = -10`

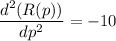
At p = 155

`(d^2(R(p)))/(dp^2) < 0`

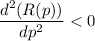
Thus by double derivative test, maxima occurs at p = 155 for R(p).

Thus, maximum revenue occurs when p = $155.

Maximum revenue

`R(155) = -5(155)^2 + 1550(155) = 120125`

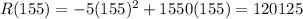
Thus, maximum revenue is $120125 that occurs when the unit price is $155.