Answer:
Explanation:
Given
Plane travels 240 miles
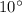 East of North
East of North
Position vector
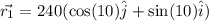
Then the plane travels 180 miles
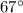 East of North
East of North
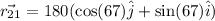
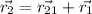
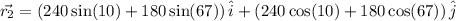
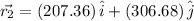
Total distance traveled in North direction is given by coefficient of \hat{j}
i.e. North

Total distance traveled in East direction is given by coefficient of \hat{i}
East
