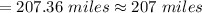Question

A plane travels 240 miles on a bearing of N 10° E and then changes its course to N 67° E and travels another 180 miles. Find the total distance traveled north and the total distance traveled east. (Round each answer to the nearest whole number.)

Answer 1

Explanation:

Given

Plane travels 240 miles
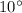`10^(\circ)` East of North

Position vector
`\vec{r_1}=240(\cos(10)\hat{j}+\sin (10)\hat{i})`

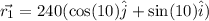
Then the plane travels 180 miles
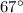`67^(\circ)` East of North

`\vec{r_(21)}=180(\cos(67)\hat{j}+\sin (67)\hat{i})`

`\vec{r_2}=\vec{r_(21)}+\vec{r_1}`

`\vec{r_2}=\left ( 240\sin (10)+180\sin (67)\right )\hat{i}+\left ( 240\cos (10)+180\cos (67)\right )\hat{j}`

`\vec{r_2}=\left ( 207.36\right )\hat{i}+\left ( 306.68\right )\hat{j}`

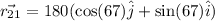
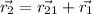
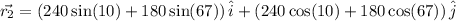
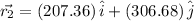
Total distance traveled in North direction is given by coefficient of \hat{j}

i.e. North
`=306.68\ miles\approx 307\ miles`

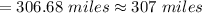
Total distance traveled in East direction is given by coefficient of \hat{i}

East
`=207.36\ miles\approx 207\ miles`