Question

Three students were applying to the same graduate school. They came from schools with different grading systems. Which student had the best GPA when compared to other students at his school? Explain how you determined your answer. Student GPA School Average GPA School Standard Deviation Thuy 2.7 3.2 0.8 Vichet 87 75 20 Kamala 8.6 8 0.4

Answer 1

Kamala had the higher Z-score, so she had the best GPA when compared to other students at his school.

Explanation:

Problems of normally distributed samples can be solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

In this problem, we have that:

Three students, graded on different curves. I will find whoever has the higher Z-score, and this is the one which had the best GPA.

Thuy 2.7 3.2 0.8

So the student GPA is 2.7, the Average GPA at the school was 3.2 and the standard deviation was 0.8.

`Z = (X - \mu)/(\sigma)`

`Z = (2.7 - 3.2)/(0.8)`

`Z = -0.625`

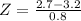
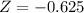
Vichet 87 75 20

So the student GPA is 87, the Average GPA at the school was 75 and the standard deviation was 20.

`Z = (X - \mu)/(\sigma)`

`Z = (87 - 75)/(20)`

`Z = 0.6`

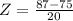
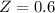
Kamala 8.6 8 0.4

So the student GPA is 8.6, the Average GPA at the school was 8 and the standard deviation was 0.4.

`Z = (X - \mu)/(\sigma)`

`Z = (8.6 - 8)/(0.4)`

`Z = 1.5`

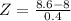
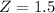
Kamala had the higher Z-score, so she had the best GPA when compared to other students at his school.