Question

Assume that your parents wanted to have $100,000 saved for college by your 18th birthday and they started saving on your first birthday. They saved the same amount on your birthday and earned 8.0% per year on their investments.

A. How much would they have to save each year to reach their goal?

B. If they think you will take five years instead of four to graduate to graduate and decide to have $140,000 saved just in case, how much more would they have to save each year to reach their new goal?

Answer 1

My parents will need to make 18 deposits of 24,724.16 dollars

My parent will then have to deposit 28,185.55 per year

which is $3,461.39 more than the other scenario

Step-by-step explanation:

We need to solve for the future value of an annuity-due (because the payment are made at the beginning of each period

`FV / ((1+r)^(time) -1 )/(rate)(1+r) = C\\`

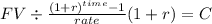
FV 1,000,000

time 18

rate 0.08

`1,000,000 / ((1+0.08)^(18)-1 )/(0.08)(1+0.08) = C\\`

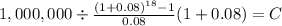
C $ 24,724.163

If we need do save and additional 140,000 dollars:

`FV / ((1+r)^(time) -1 )/(rate)(1+r) = C\\`

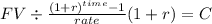
FV 1,140,000

time 18

rate 0.08

`1,140,000 / ((1+0.08)^(18)-1 )/(0.08)(1+0.08) = C\\`

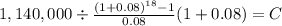
C $ 28,185.546

The difference will be:

28,185.55 - 24,724.16 = 3.461,39‬