There will be 231 handshakes in total
Solution:
There are 22 people in a room
Everyone shakes everyone else’s hand exactly one time
To find: Total number of handshakes in total
Let,
n = total number of people that will shake hands
but since all (total) can't shake hands with themselves, hence we subtract one individual to start the handshaking
(n - 1) = people would each shake hands
hence we multiply both total number persons with people that will shake hands;
n(n - 1)
but that counts every handshake twice, so we have to divide by 2
Therefore;
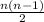
Here, n = 22
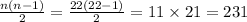
Thus there will be 231 handshakes in total