One revolution corresponds to an angular displacement of
 , so its angular speed is
, so its angular speed is
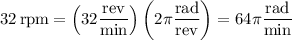
 radians is equivalent to 180 degrees, so the angular speed could also be
radians is equivalent to 180 degrees, so the angular speed could also be
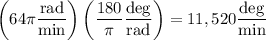
The linear speed depends on the wheel's radius. Suppose its radius is
 . Then the wheel has circumference
. Then the wheel has circumference
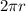 units. A point on the edge of the wheel travels this distance in one revolution, so its linear speed is
units. A point on the edge of the wheel travels this distance in one revolution, so its linear speed is
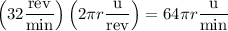
(where
 stands for units of length)
stands for units of length)