Answer:
The measure of 'x' is 6 units.
Explanation:
Given:
An isosceles triangle.
The two equal arms length =
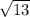
Measure of the altitude =
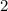
Note:The altitude to the base of an isosceles triangle bisects the base.
The altitude also forms 90 degree at the base.
So, the base length can also be seen as 'x' which we can also be written as
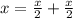
And
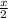 is a part of the right angled triangle.
is a part of the right angled triangle.
Where hypotenuse =
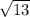
Perpendicular length =
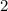
Base length =
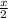
Now,
From Pythagoras formula we know that:
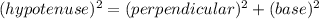
Plugging the values:
⇒
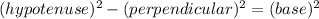
⇒
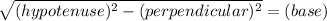
⇒
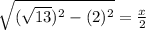
⇒
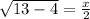
⇒
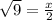
⇒
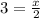
⇒
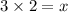
⇒
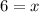
So the value of base 'x' = 6 units.
Option D is the rigth choice.