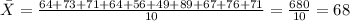Answer:
Students who studied
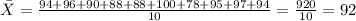
Students who did not study
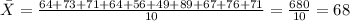
The answer would be:
92,68
Explanation:
For this case we have the following data:
Students who studied
Exam grade: 94 96 90 88 88 100 78 95 97 94
The sample mean is calculated with the following formula:
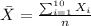
And if we replace the values given we got:
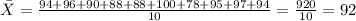
Students who did not study
Exam grade: 64 73 71 64 56 49 89 67 76 71
The sample mean is calculated with the following formula:
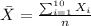
And if we replace the values given we got: