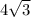Question:
In the right triangle shown, ∠B=60° and BC = 2√3
How long is AB?
Answer exactly, using a radical if needed.
The image of the triangle is attached below:
Answer:
The length of AB is
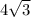
Step-by-step explanation:
It is given that ∠B = 60° and BC =

To determine the length of AB, we shall use the cosine formula.
Because the value of the angle and its adjacent side is given and AB is the hypotenuse, we shall substitute the value of angle and adjacent side in the formula to find the value of AB.
Thus, the formula for
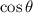 is given by
is given by
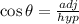
Where
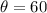 and
and
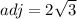 and
and
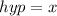
Substituting these values in the formula, we get,
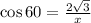
Interchanging, we get,
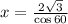
The value of
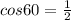
Substituting, we get,
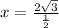
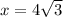
Thus, the value of x is
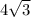
Hence, the length of the hypotenuse AB is