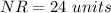Question

Triangle MNO is an equilateral triangle with sides measuring 16 StartRoot 3 EndRoot units. Triangle M N O is an equilateral triangle with sides measuring 16 StartRoot 3 EndRoot units. A perpendicular bisector is drawn from point N to point R on side M O splitting side M O into 2 equal parts. What is the height of the triangle? 12 units 24 units 36 units 72 units

Answer 1

b 24

Explanation:

Answer 2

The correct option is second one i.e 24 units.

Therefore the height of the triangle is

`NR=24\ units`

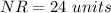
Explanation:

Given:

An equilateral triangle has all sides equal.

ΔMNO is an Equilateral Triangle with sides measuring,

`NM = MO = ON =16√(3)`

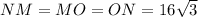
NR is perpendicular bisector to MO such that

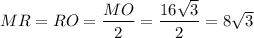`MR=RO=(MO)/(2)=(16√(3))/(2)=8√(3)` .NR ⊥ Bisector.

To Find:

Height of the triangle = NR = ?

Solution :

Now we have a right angled triangle NRM at ∠R =90°,

So by applying Pythagoras theorem we get

`(\textrm{Hypotenuse})^(2) = (\textrm{Shorter leg})^(2)+(\textrm{Longer leg})^(2)`

Substituting the values we get

`(MN)^(2) = (MR)^(2)+(NR)^(2)\\\\(16√(3))^(2)=(8√(3))^(2)+(NR)^(2)\\\\(NR)^(2)=768-192=576\\Square\ rooting\ we\ get\\NR=√(576)=24\ units`

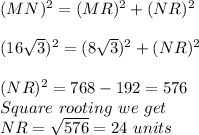
Therefore the height of the triangle is

`NR=24\ units`