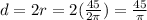Question

A slice of pizza whose edges form a 32degrees angle with an outer crust edge 4 inches long was found in a gym locker. What was the diameter of the original​ pizza?g

Answer 1

The diameter was
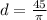`d=(45)/(\pi )` in.

Explanation:

The arc of a circle is given by

`s=r\theta`

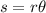
where

s = arc length

r = radius of the circle

θ = measure of the central angle in radians.

From the information given

s = 4 in

θ = 32º

To find the diameter of the original​ pizza, we use the formula of the diameter of a circle

`d=2r`

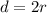
First, we need to convert the angle to radians

`\theta=32\º \cdot (\pi)/(180\º) =(8\pi )/(45)`

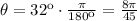
Next, solve for r from the arc formula

`r=(s)/(\theta) =(4)/((8\pi )/(45)) =(45)/(2\pi )`

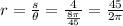
Then, we use the diameter of a circle formula

`d=2r=2((45)/(2\pi ))=(45)/(\pi )`