Question

A 200-g block is attached to a horizontal spring and executes simple harmonic motion with a period of 0.250 s. The total energy of the system is 2.00 J. Find (a) the force constant of the spring and (b) the amplitude of the motion.

Answer 1

(A) Spring constant will be 126.58 N/m

(B) Amplitude will be equal to 0.177 m

Step-by-step explanation:

We have given mass of the block m = 200 gram = 0.2 kg

Time period T = 0.250 sec

Total energy is given TE = 2 J

(A) For mass spring system time period is equal to
`T=2\pi \sqrt{(m)/(K)}`

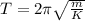
So
`0.250=2* 3.14 \sqrt{(0.2)/(K)}`

`0.0398=\sqrt{(0.2)/(K)}`

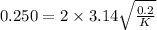
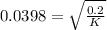
Now squaring both side

`0.00158=(0.2)/(K)`

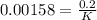
K = 126.58 N/m

So the spring constant of the spring will be 126.58 N/m

(B) Total energy is equal to
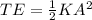`TE=(1)/(2)KA^2`, here K is spring constant and A is amplitude

So
`2=(1)/(2)* 126.58* A^2`

`A^2=0.0316`

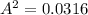
A = 0.177 m

So the amplitude of the wave will be equal to 0.177 m