Answer:
340 of the adults in the sample voted.
The 95% confidence interval estimate of the population percent of Americans that vote is (0.6391, 0.7209). This means that we are 95% sure that the true proportion of Americans that vote is between 0.6391 and 0.7209.
Explanation:
In 2008, a random sample of 500 american adults was take and we found that 68% of them voted. How many of the 500 adults in the sample voted?
This is 68% of 500.
So 0.68*500 = 340.
340 of the adults in the sample voted.
Now construct a 95% confidence interval estimate of the population percent of Americans that vote and write a sentence to explain the confidence interval.
In a sample with a number n of people surveyed with a probability of a success of
 , and a confidence interval
, and a confidence interval
 , we have the following confidence interval of proportions.
, we have the following confidence interval of proportions.

In which
Z is the zscore that has a pvalue of
 .
.
For this problem, we have that:
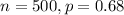
95% confidence interval
So
 , z is the value of Z that has a pvalue of
, z is the value of Z that has a pvalue of
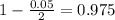 , so
, so
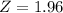 .
.
The lower limit of this interval is:
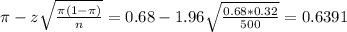
The upper limit of this interval is:
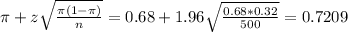
The 95% confidence interval estimate of the population percent of Americans that vote is (0.6391, 0.7209). This means that we are 95% sure that the true proportion of Americans that vote is between 0.6391 and 0.7209.