Question

A baseball player friend of yours wants to determine his pitching speed. You have him stand on a ledge and throw the ball horizontally from an elevation 6.0 m above the ground. The ball lands 25 m away.

What is his pitching speed?

Answer 1

To solve this problem we will apply the concepts related to the kinematic equations of linear motion. Punctually we will verify the vertical displacement and the horizontal displacement from their respective components. We will start by calculating the time it took to reach the objective and later with that time, we will find the horizontal velocity launch component. The position can be written as,

`h= v_(0y)t+(1)/(2)a_yt^2`

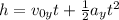
Here,

h = Height

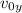`v_(0y)`= Initial velocity in vertical direction

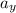`a_(y)` = Vertical acceleration (At this case, due to gravity)

`t` = Time

There is not vertical velocity because the ball was thrown horizontally), then we have that

`6= (0)t+(1)/(2)(9.8)t^2`

`t = 1.1065s`

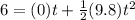
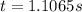
Now using the equation of horizontal motion we have with this time that the initial velocity was,

`x = v_(ox)t+(1)/(2)a_xt^2`

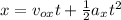
Here,

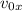`v_(0x)`= Horizontal initial velocity

`t` = Time

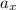`a_x` = Acceleration in horizontal plane

There is not acceleration in horizontal plane, only in vertical plane, then we have

`25= v_(0x)(1.1065)+(1)/(2)(0)(1.1065)^2`

`v_(0x) = 22.5938m/s`

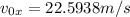
Therefore the pitching speed is 22.5938m/s