Question

Joe gave 1/4 of his total candies to his classmate then he gave 4/6 of when he had left to his brother when he went home then he realized that you didn’t give any to his sister he gave 25% of the remaining candies to her after all this he realized that he only had 21 candies left how many candies did he have In the beginning

Answer 1

112

Explanation:

Given: Joe gave 1/4 of his total candies to his classmate.

Then, he gave 4/6 of when he had left to his brother.

He gave 25% of the remaining candies to his sister.

Finally, he only had 21 candies left.

Lets assume the total number of candies at the beginning be "x".

First, finding the number candies left after giving candies to classmate.

∴ Remaining candies=
`x- x* (1)/(4)`

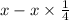
Solving it to find remaining candies after giving candies to clasmate.

⇒ Remaining candies=
`x-(x)/(4)`

Taking LCD as 4

⇒ Remaining candies=
`(4x-x)/(4) = (3x)/(4)`

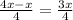
∴ Remaining candies after giving candies to clasmate=
`(3x)/(4)`

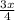
now, finding the candies left after giving candies to his brother.

∴ Remaining candies=
`(3x)/(4) - (3x)/(4) * (4)/(6)`

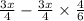
Solving it to find the remaining candies after giving candies to his brother.

⇒ Remaining candies=
`(3x)/(4) - (x)/(2)`

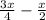
Taking LCD 4

⇒ Remaining candies=
`(3x-2x)/(4) = (x)/(4)`

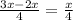
∴ Remaining candies after giving candies to his brother=
`(x)/(4)`

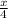
We know, Joe was left with only 21 candies after giving candies to his sister.

Therefore, putting an equation for remaining candies to find the number of candies at the beginning.

⇒
`(x)/(4) - 25\% * (x)/(4) = 21`

⇒
`(x)/(4) - (0.25x)/(4) = 21`

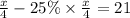
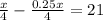
Taking LCD 4

⇒
`(x-0.25x)/(4) = 21`

⇒
`(0.75x)/(4) = 21`

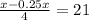
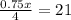
Multiplying both side by 4

⇒
`0.75x= 21* 4`

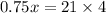
dividing both side by 0.75

⇒
`x= (21* 4)/(0.75)`

∴
`x= 112`

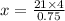
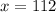
Hence, Joe had 112 candies at the beginning.