Answer:
Part a: The Future value of the annuity after 40 years is $518113.24.
Part b: The per year withdrawal in retirement for 25 years will be $48536.19.
Explanation:
As the numbers are appearing as a duplication taking all these values as single.
Part a
Future value is given as
![FV=PMT * [\frac{{(1+I)}^(N)-1}{I}]](https://img.qammunity.org/2021/formulas/mathematics/college/5prl4al3o9knr7h1osdqv0fsb85e7bc2ig.png)
Here
- PMT is the annual value which is $2000 per year
- I is the interest rate which is given as 8%
- N is 40
![FV=PMT * [\frac{{(1+I)}^(N)-1}{I}]\\\\FV=2000 * [\frac{({1+.08})^(40)-1}{.08}]\\FV=\$ 518113.03](https://img.qammunity.org/2021/formulas/mathematics/college/zeaa7e8oprg99fttg3c2ih2suigllt69kg.png)
So the Future value of the annuity after 40 years is $518113.24.
Part b
Per year withdrawal is given as
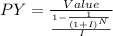
Here
- PY is the per year withdrawal
- Value is the total amount which is $ 518113 as calculated in part a
- I is the rate of interest which is 8%
- N is 25 years as expected life to live in retirement.
So the value is given as
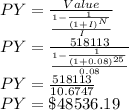
So the per year withdrawal in retirement for 25 years will be $48536.