Question

A pipe produces successive harmonics at 300 Hz and 350 Hz. Calculate the length of the pipe and state whether it is closed at one end or not. Assume the speed of sound to be 340 m/s.

Answer 1

The pipe is open ended and the length of pipe is 3.4 m.

Step-by-step explanation:

For identification of the type of pipe checking the successive frequencies in both the open pipe and closed pipe as below

Equation for nth frequency for open end pipe is given as

`f_n=(nv)/(2L)`

For (n+1)th value the frequency is

`f_(n+1)=((n+1)v)/(2L)`

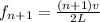
Taking a ratio of both equation and solving for n such that the value of n is a whole number

`(f_(n+1))/(f_n)=(((n+1)v)/(2L))/((nv)/(2L))\\(350)/(300)=((n+1))/(n)\\350n =300n+300\\50n =300\\n =6\\`

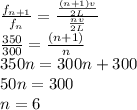
So n is a whole number this means that the pipe is open ended.

For confirmation the nth frequency for a closed ended pipe is given as

`f_n=((2n+1)v)/(4L)`

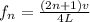
For (n+1)th value the frequency is

`f_(n+1)=((2n+3)v)/(4L)`

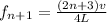
Taking a ratio of both equation and solving for n such that the value of n is a whole number

`(f_(n+1))/(f_n)=(((2n+3)v)/(2L))/(((2n+1)v)/(2L))\\(350)/(300)=((2n+3))/((2n+1))\\700n+350 =600n+900\\100n =550\\n =5.5\\`

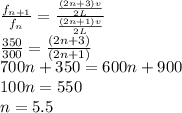
As n is not a whole number so this is further confirmed that the pipe is open ended.

Now from the equation of, with n=6, v=340 m/s and f=300 Hz

`f_n=(nv)/(2L)\\300=(6 * 340)/(2L)\\L=(2040)/(600)\\L=3.4 m`

The value of length is 3.4m.