Answer:
The first set: 8, 15, and 17.
Explanation:
Pair: 8, 15, 17
By the pythagorean theorem, a triangle is a right triangle if and only if
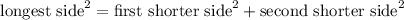 .
.
In this case,
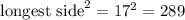 .
.
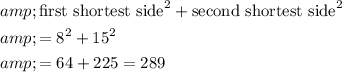 .
.
In other words, indeed
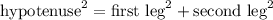 . Hence, 8, 15, 17 does form a right triangle.
. Hence, 8, 15, 17 does form a right triangle.
Similarly, check the other pairs. Keep in mind that the square of the longest side should be equal to the sum of the square of the two
Pair: 10, 15, 20
Factor out the common factor
 to simplify the calculations.
to simplify the calculations.
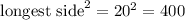
 .
.
 .
.
Hence, by the pythagorean theorem, these three sides don't form a right triangle.
Pair: 12, 18, 22
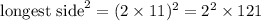 .
.
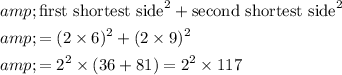 .
.
 .
.
Hence, by the pythagorean theorem, these three sides don't form a right triangle.
Pair: 7, 9, 11
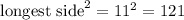 .
.
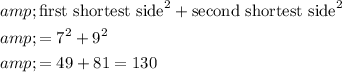 .
.
 .
.
Hence, by the pythagorean theorem, these three sides don't form a right triangle.