Question

An eagle is flying from point A to point B in order to catch a sparrow. Its flying trajectory is a parabola shape

that has the equation y = -5(x+6) +10, where x and y are measured in meters. If the eagle is at a height of

20 meters, how far away are the two points from one another?

Answer 1

3 meters

Explanation:

Answer 2

From 10 to 20 meters.

Explanation:

1) If the sparrow has a parabolic trajectory then it must be actually:

`y=-5\left ( x+6 \right )^(2)+10`

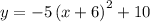
2) If the eagle is at 20 meters high, then we write:

`y=20`

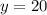
Since the exact x coordinate was not given.

But since it wants to get the sparrow

3) If we expand the equation we have:

`-5x^(2)-60x-170=0\\\\X_(v)=(-b)/(2a)=(60)/(-10) = -6\\Y_(v)=(-\Delta)/(4a) =(-200)/(-20) =10`

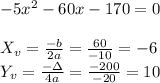
Since the maximum point is equal to 10. The distance where the sparrow is flying ranges from 10 to 20 meters to the eagles spot.

`10\leq d \leq20 \:or \:[10,20]`

4) Since the x coordinate was not given then we can neither precisely calculate the distance where A is nor where B is located.