Question

The diameters of bearings used in an aircraft landing gear assembly have a standard deviation of ???? = 0.0020 cm. A random sample of 15 bearings has an average diameter of 8.2535 cm. Please (a) test the hypothesis that the mean diameter is 8.2500 cm using a two-sided alternative and ???? = 0.05; (b) find P-value for the test; and (c) construct a 95% two-sided confidence interval on the mean diameter.

Answer 1

a

b

c

Explanation:

Answer 2

(a) We conclude after testing that mean diameter is 8.2500 cm.

(b) P-value of test = 2 x 0.0005% = 1 x
`10^(-5)` .

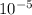(c) 95% confidence interval on the mean diameter = [8.2525 , 8.2545]

Explanation:

We are given with the population standard deviation,
`\sigma` = 0.0020 cm

Sample Mean, Xbar = 8.2535 cm and Sample size, n = 15

(a) Let Null Hypothesis,
`H_0` : Mean Diameter,
`\mu` = 8.2500 cm

Alternate Hypothesis,
`H_1` : Mean Diameter,
`\mu`
`\\eq` 8.2500 cm{Given two sided}

So, Test Statistics for testing this hypothesis is given by;

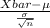`(Xbar-\mu)/((\sigma)/(√(n) ) )` follows Standard Normal distribution

After putting each value, Test Statistics =
`(8.2535-8.2500)/((0.0020)/(√(15) ) )` = 6.778

Now we are given with the level of significance of 5% and at this level of significance our z score has a value of 1.96 as it is two sided alternative.

Since our test statistics does not lie in the rejection region{value smaller than 1.96} as 6.778>1.96 so we have sufficient evidence to accept null hypothesis and conclude that the mean diameter is 8.2500 cm.

(b) P-value is the exact % where test statistics lie.

For calculating P-value , our test statistics has a value of 6.778

So, P(Z > 6.778) = Since in the Z table the highest value for test statistics is given as 4.4172 and our test statistics has value higher than this so we conclude that P - value is smaller than 2 x 0.0005% { Here 2 is multiplied with the % value of 4.4172 because of two sided alternative hypothesis}

Hence P-value of test = 2 x 0.0005% = 1 x
`10^(-5)` .

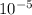(c) For constructing Two-sided confidence interval we know that:

Probability(-1.96 < N(0,1) < 1.96) = 0.95 { This indicates that at 5% level of significance our Z score will lie between area of -1.96 to 1.96.

P(-1.96 <
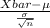`(Xbar-\mu)/((\sigma)/(√(n) ) )` < 1.96) = 0.95

P(
`-1.96(\sigma)/(√(n) )` <
`Xbar - \mu` <
`1.96(\sigma)/(√(n) )` ) = 0.95

P(
`-Xbar-1.96(\sigma)/(√(n) )` <
`-\mu` <
`1.96(\sigma)/(√(n) )-Xbar` ) = 0.95

P(
`Xbar-1.96(\sigma)/(√(n) )` <
`\mu` <
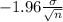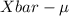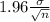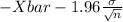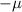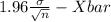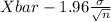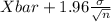`Xbar+1.96(\sigma)/(√(n) )`) = 0.95

So, 95% confidence interval for
`\mu` = [
`Xbar-1.96(\sigma)/(√(n) )` ,
`Xbar+1.96(\sigma)/(√(n) )`]

= [
`8.2535-1.96(0.0020)/(√(15) )` ,
`8.2535+1.96(0.0020)/(√(15) )`]

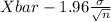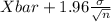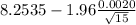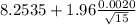= [8.2525 , 8.2545]

Here
`\mu` = mean diameter.

Therefore, 95% two-sided confidence interval on the mean diameter

= [8.2525 , 8.2545] .