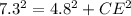Question

In the figure below, the segments cd and ce are tangent to the circle centered at o. Given that od= 4.8 and oc= 7.3, find ce

Answer 1

`CE=5.5\ units`

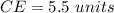
Explanation:

The picture of the question in the attached figure

we know that

According to the Perpendicular Tangent Theorem, tangent lines are always perpendicular to a circle's radius at the point of intersection

That means ----> Triangles ODC and OEC are right triangles

In the right triangle OEC

we have

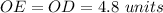`OE=OD=4.8\ units` ----> radius of the circle

`OC=7.3\ units`

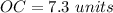
Applying the Pythagorean Theorem

`OC^2=OE^2+CE^2`

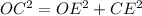
substitute the given values

`7.3^2=4.8^2+CE^2`

`CE^2=7.3^2-4.8^2\\CE^2=30.25\\CE=5.5\ units`