Question

Industrial engineers periodically conduct "work measurement" analyses to determine the time required to produce a single unit of output. At a large processing plant, the number of total worker-hours required per day to perform a certain task was recorded for 50 days. a. Compute the mean, median, and mode of the data set. b. Find the range, variance, and standard deviation of the data set. c. Construct the intervals using the Empirical rule. d. Find the 70th percentile for the data on total daily worker-hours.

Answer 1

a)
`\bar X =117.8`

`Median= (117+118)/(2)=117.5`

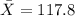
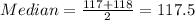
The mode on this case is the most repeated value 128 with a frequency of 3

b)
`Range = Max -Min = 150-88=62`

`s^2 = 225.334`

`s= √(225.334)= 15.011`

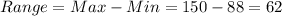
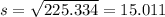
c)
`y \pm s`

`Lower = 117.8 -15.011=102.809`

`Upper = 117.8 +15.011=132.831`

`y \pm 2s`

`Lower = 117.8 -2*15.011=87.797`

`Upper = 117.8 +2*15.011=147.842`

`y \pm 3s`

`Lower = 117.8 -3*15.011=72.787`

`Upper = 117.8 +3*15.011=162.85`

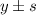
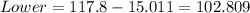
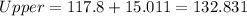
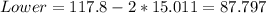
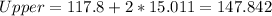
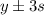
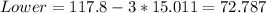
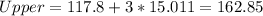
d) For this case we can calculate the position where we have accumulated 70% of the data below.

50*0.7 = 35

So on the position 35th from the dataset ordered we see that the value is 128 and this value would represent the 70th percentile on this case.

Explanation:

For this case we consider the following data:

128,119,95,97,124,128,142,98,108,120,113,109,124,132,97,138,133,136,120,112,146,128,103,135,114,109,100,111,131,113,124,131,133,131,88,118,116,98,112,138,100,112,111,150,117,122,97,116,92,122

Part a

For this case we can calculate the mean with the following formula:

`\bar X = (\sum_(i=1)^(50) X_i)/(50)`

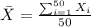
And after replace we got
`\bar X =117.8`

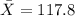
In order to calculate the median first we order the dataset and we got:

88 92 95 97 97 97 98 98 100 100 103 108 109 109 111 111 112 112 112 113 113 114 116 116 117 118 119 120 120 122 122 124 124 124 128 128 128 131 131 131 132 133 133 135 136 138 138 142 146 150

The median would be the average between the position 25 and 26 from the data ordered and we got:

`Median= (117+118)/(2)=117.5`

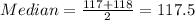
The mode on this case is the most repeated value 128 with a frequency of 3

Part b

the range is defined as the difference between the maximun and minimum so we got:

`Range = Max -Min = 150-88=62`

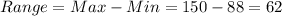
The sample variance can be calculated with this formula:

`s^2 = (\sum_(i=1)^n (X_i -\bar X)^2)/(n-1)`

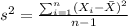
And after calculate we got:
`s^2 = 225.334`

And the deviation is just the square root of the variance and we got:

`s= √(225.334)= 15.011`

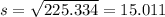
Part c

For this case we can construct the interval with 1 , 2 and 3 deviation from the mean like this:

`y \pm s`

`Lower = 117.8 -15.011=102.809`

`Upper = 117.8 +15.011=132.831`

`y \pm 2s`

`Lower = 117.8 -2*15.011=87.797`

`Upper = 117.8 +2*15.011=147.842`

`y \pm 3s`

`Lower = 117.8 -3*15.011=72.787`

`Upper = 117.8 +3*15.011=162.85`

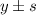
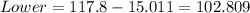
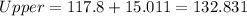
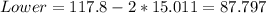
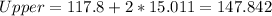
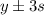
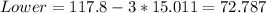
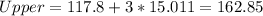
Part d

For this case we can calculate the position where we have accumulated 70% of the data below.

50*0.7 = 35

So on the position 35th from the dataset ordered we see that the value is 128 and this value would represent the 70th percentile on this case.