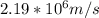Question

In the Bohr model the hydrogen atom consists of an electron in a circular orbit of radius a 0 = 5.29 × 10 − 11 m around the nucleus. Using this model, and ignoring relativistic effects, what is the speed of the electron?

Answer 1

To solve this problem we will apply the concept of balance of Forces in the body. For such an effect the centripetal force must be equivalent to the electrostatic force of the body, therefore

`F_c = F_e`

`(mv^2)/(r) = k (q_pq_e)/(r^2)`

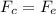
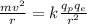
Here

m = Mass of electron

r = Distance between them

k = Coulomb's constant

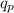`q_p` = Charge of proton

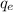`q_e` = Charge of electron

v = Velocity

Rearranging to find the velocity we have that,

`v^2 = (kq_pq_e)/(mr)`

`v = \sqrt{(kq_pq_e)/(mr)}`

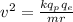
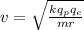
Replacing,

`v = \sqrt{((9*10^9)(1.6*10^(-19))(1.6*10^(-19)))/((9.1*10^(-31))(5.29*10^(-11)))}`

`v = 2.19*10^6m/s`

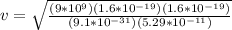
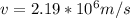
Therefore the speed of the electron is
`2.19*10^6m/s`