Question

Steve likes to entertain friends at parties with "wire tricks." Suppose he takes a piece of wire 60 inches long and cuts it into two pieces. Steve takes the first piece of wire and bends it into the shape of a perfect circle. He then proceeds to bend the second piece of wire into the shape of a perfect square. What should the lengths of the wires be so that the total area of the circle and square combined is as small as possible? (Round your answers to two decimal places.)

Answer 1

a) the length of the wire for the circle =
`((60\pi )/(\pi+4)) in`

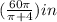
b)the length of the wire for the square =
`((240)/(\pi+4)) in`

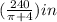
c) the smallest possible area = 126.02 in² into two decimal places

Explanation:

If one piece of wire for the square is y; and another piece of wire for circle is (60-y).

Then; we can say; let the side of the square be b

so 4(b)=y

b=
`(y)/(4)`

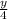
Area of the square which is L² can now be said to be;

`A_S=((y)/(4))^2 = (y^2)/(16)`

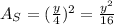
On the otherhand; let the radius (r) of the circle be;

2πr = 60-y

`r = (60-y)/(2\pi )`

Area of the circle which is πr² can now be;

`A_C= \pi ((60-y)/(2\pi ) )^2`

`=( (60-y)/(4\pi ) )^2`

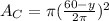
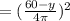
Total Area (A);

A =
`A_S+A_C`

=
`(y^2)/(16) +((60-y)/(4\pi ) )^2`

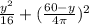
For the smallest possible area;
`(dA)/(dy)=0`

∴
`(2y)/(16)+(2(60-y)(-1))/(4\pi)=0`

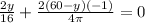
If we divide through with (2) and each entity move to the opposite side; we have:

`(y)/(18)=((60-y))/(2\pi)`

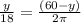
By cross multiplying; we have:

2πy = 480 - 8y

collect like terms

(2π + 8) y = 480

which can be reduced to (π + 4)y = 240 by dividing through with 2

`y= (240)/(\pi+4)`

∴ since
`y= (240)/(\pi+4)`, we can determine for the length of the circle ;

60-y can now be;

=
`60-(240)/(\pi+4)`

=
`((\pi+4)*60-240)/(\pi+40)`

=
`(60\pi+240-240)/(\pi+4)`

=
`((60\pi)/(\pi+4))in`

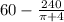
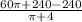
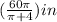
also, the length of wire for the square (y) ;
`y= ((240)/(\pi+4))in`

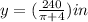
The smallest possible area (A) =
`(1)/(16) ((240)/(\pi+4))^2+((60\pi)/(\pi+y))^2((1)/(4\pi))`

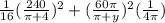
= 126.0223095 in²

≅ 126.02 in² ( to two decimal places)