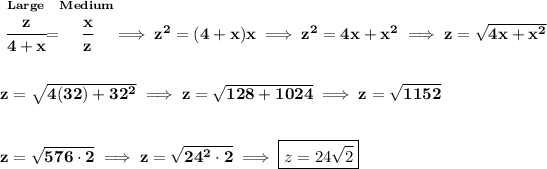Question

Number 24 only please help me please

Answer 1

Check the picture below.

the idea being, that if we run an altitude segment from a right-angle in a triangle, and parallel to the opposite side, like in thise case, we end up with 3 similar triangles, a Large one, containing the other smaller ones, a Medium and a Small.

now, let's simply use proportions for those similar triangles.

`\bf \stackrel{Large}{\cfrac{12}{4+x}}=\stackrel{Small}{\cfrac{4}{12}}\implies \cfrac{12}{4+x}=\cfrac{1}{3}\implies 36=4+x\implies \boxed{32=x} \\\\[-0.35em] ~\dotfill\\\\ \stackrel{Small}{\cfrac{4}{y}}=\stackrel{Medium}{\cfrac{y}{x}}\implies 4x=y^2\implies 4(32)=y^2\implies 128=y^2\implies √(128)=y \\\\\\ √(64\cdot 2)=y\implies √(8^2\cdot 2)=y\implies \boxed{8√(2)=y} \\\\[-0.35em] ~\dotfill`

`\bf \stackrel{Large}{\cfrac{z}{4+x}}=\stackrel{Medium}{\cfrac{x}{z}}\implies z^2=(4+x)x\implies z^2=4x+x^2\implies z = √(4x+x^2) \\\\\\ z = √(4(32)+32^2)\implies z = √(128+1024)\implies z = √(1152) \\\\\\ z = √(576\cdot 2)\implies z = √(24^2\cdot 2)\implies \boxed{z = 24√(2)}`