Question

The following are prices for a 25 inch T.V. found in different stores around Roseville: 100,98,121,111,97,135,136,104,135,138,189,114, 92, 69 Describe the distribution. a. Skewed to the right b. Symmetric c. Skewed to the left d. Uniform e. Bell shaped

Answer 1

(c) Skewed to the left

Explanation:

To describe the distribution of the data determine the mean, median and mode.

The provided data arranged in ascending order is:

{69, 92, 97, 98, 100, 104, 111, 114, 121, 135, 135, 136, 138, 189}

• Mean:

`Mean=(Sum\ of\ observations)/(Number\ of\ observations)\\ =(69+92+97+ 98+ 100+ 104+ 111+ 114+ 121+ 135+ 135+ 136+ 138+ 189)/(14) \\=117.07`

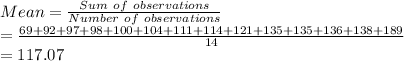
• Median: As the number of observations is even the median of the data will be the mean of the middle two values, when the data is arranged in ascending order.

`Median=Mean (7^(th), 8^(th)\ observation)\\=(7^(th)\ obs.+8^(th)\ obs.)/(2)\\ =(111+114)/(2)\\ =112.5`

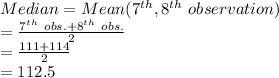
• Mode of the data is the value with the highest frequency.

The value 135 has the highest frequency of 2.

`Mode=135`

So Mean < Mode and Median < Mode.

For a distribution that is skewed to the left the mean and median is less than the mode of the data.

Thus, the data is left-skewed.