How many extraneous solutions does the equation below have? StartFraction 9 Over n squared + 1 EndFraction = StartFraction n + 3 Over 4 EndFraction 0 1 2 3

Question

asked Jul 15, 2021 131k views

2 Answers

ORole · Answer 1 · 2021-07-16T13:45:11+0000

Answer:

A. 0

Explanation:

How many extraneous solutions does the equation below have?

StartFraction 9 Over n squared + 1 EndFraction = StartFraction n + 3 Over 4 EndFraction

0

1

2

3

Kawnah · Answer 2 · 2021-07-21T17:03:58+0000

Answer:

We can say that the given equation has no extraneous solutions.

The correct option is A.) 0

Explanation:

the given equation is
(9)/(n^(2) +1) = (n+3)/(4)

this equals to
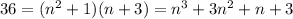
36 = (n^(2) +1)(n+3) = n^(3) + 3n^(2) + n + 3

therefore
$n^(3) +3n^(2) +n+3 = 36 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}n^(3) +3n^(2) +n-33=0$

Solving the equation through Newton-Raphson method we get n
$\approx$ 2.3845.

We can say that the given equation has no extraneous solutions.