Question

Using your knowledge of exponential and logarithmic functions and properties, what is the intensity of a fire alarm that has a sound level of 120 decibels?

A.
1.0x10^-12 watts/m^2
B.
1.0x10^0 watts/m^2
C.
12 watts/m^2
D.
1.10x10^2 watts/m^2

Answer 1

Option B:

`I=1.0*\ 10^(0) \ \text {watts}/ \text m^2}`

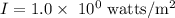
Solution:

Given sound level = 120 decibel

To find the intensity of a fire alarm:

`$\beta=10\log\left((I)/(I_0) \right)`

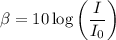
where
`I_0=1*10^(-12)\ \text {watts}/ \text m^2}`

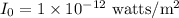
Step 1: First divide the decibel level by 10.

120 ÷ 10 = 12

Step 2: Use that value in the exponent of the ratio with base 10.

`10^(12)`

Step 3: Use that power of twelve to find the intensity in Watts per square meter.

`$10^(12)=\left((I)/(I_0) \right)`

`$10^(12)=\left(\frac{I}{1*10^(-12)\ \text {watts}/ \text m^2} \right)`

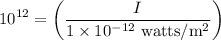
Now, do the cross multiplication,

`I=10^(12)*1*\ 10^(-12) \ \text {watts}/ \text m^2}`

`I=1*\ 10^(12-12) \ \text {watts}/ \text m^2}`

`I=1*\ 10^(0) \ \text {watts}/ \text m^2}`

`I=1.0*\ 10^(0) \ \text {watts}/ \text m^2}`

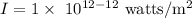
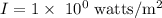
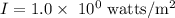
Option B is the correct answer.

Hence
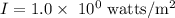`I=1.0*\ 10^(0) \ \text {watts}/ \text m^2}`.