To solve this problem we will apply the principles of energy conservation. The kinetic energy in the object must be maintained and transformed into the potential electrostatic energy. Therefore mathematically
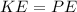

Here,
m = mass (At this case of the proton)
v = Velocity
k = Coulomb's constant
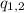 = Charge of each object
= Charge of each object
r= Distance between them
Rearranging to find the second charge we have that
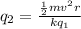
Replacing,
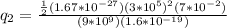

Therefore the charge on the sphere is 3.6531nC